蒙特卡洛检验是判断系统稳健性的一种方法,可以回答这样的问题:如果把历史稍作变化会怎么样?未来又会怎么样?通过蒙特卡洛检验,你可以用代表历史实际数据的一系列事件来生成另外一种略有变化的别样景象。
有些方怯用随机数据来检验某种特定现象,蒙特卡洛检验就是这类方法的统称。对不可能或很难用数学方撞来精确描述的现象来说,这种检验最为有用。蒙特卡洛这个词取自于摩纳哥的那座以赌博业闻名的城市,因为蒙特卡洛的赌场中有很多由随机事件决定结果的游戏:比如轮盘赌、掷殷子、21点等。研制原子弹的那些科学家们曾在曼哈顿计划中使用这种方棒,它的名字就来自于那个时期。
这些科学家们必须确定铀的裂变特征才能知道制造一颗原子弹需要多少铀。由于浓缩铀昂贵之极,他们承受不起判断失误的代价。如果原子弹因为铀太少而无法引爆,他们会白白浪费几个月的时间,更别说浪费多少钱了。同样的,如果他们高估了铀的用量,他们也会浪费几个月的测试时间。不幸的是,铀原子在炸弹内部的交互作用太过复杂,用当时的方怯不可能准确地建模。电脑可以完成这个任务,但那个时候还没有现在这样的电脑。
一次原子裂变会释放出大量中子,一定比例的这些中子就能引发另一次原子裂变。为了确定可裂变铀的必要用量,科学家们必须知道这个比例是多少。著名物理学家理查德·费曼(Richard Feynman)想出了一个办法:让一组数学家来研究一个中子在交互作用中的特征,据以确定这个中子究竟是被另一个原子核吸收,还是会分裂出另一个原子。费曼意识到,他们可以用随机数字来代表原子裂变时所释放出的各种中子。测试上数千次,他们就能看出铀裂变特征的准确分布规律,也就能确定铀的必要用量。费曼知道,尽管他无法预知未来,因为整个过程太过复杂,但他起码能从他熟悉的角度出发来抓住问题的主要方面,通过用随机数字模拟中子属性来获得整个问题的答案。这样,他不必准确地预测到每一个原子在每一点的运动,就能掌握铀裂变特征的本质。
别样景象
市场甚至比核裂变反应还要复杂。市场是由成千上万的人组成的,每个人都会根据自己的经验和判断来作出决策,这些决策比中子的运动特征还难预测。幸运的是,就像费曼用随机数字来分析铀一样,我们也可以借助随机数字来更好地认识一个交易系统的潜在特征,即使我们无法预见到未来。假如把过去的事情稍作变化,历史会变成什么样子?我们可以用蒙特卡洛检验来检验这种别样景象。
要用蒙特卡洛检验来生成别样景象,我们有两种常见方法可用:
交易调整
随机性地改变实际模拟结果中的交易命令和起始日,然后用调整后的交易命令和这些交易的损益水平来调整资产净值。
净值曲线调整
在初始净值曲线中随机选择一些部分,将它们组合成新的净值曲线。
在这两种方法中,净值曲线调整所生成的别样净值曲线更具现实性,因为随机改变交易命令的蒙特卡洛检验很容易低估衰落的可能性。
最大衰落总是发生在大趋势的末端或资产呈增长趋势的时期。因为在这些时候,市场之间的相关性要高于平常。期货和股票市场都是如此。当大趋势在走到尽头后崩横井逆转时,似乎所有事情都开始对你不利,即使是平常看似不相关的市场,也开始在这些起伏不定的日子相互挂钩了。
由于交易调整法去除了交易和日期的关联性,它也去除了多个同时逆转的交易对净值曲线的不利影响。这意味着蒙特卡洛检验中的衰落程度和频率要比现实中低。以2006年春季的黄金和白银走势为例。如果你检验的是一个同时涉足这两个市场的趋势跟踪系统,那么交易调整意味着你在这两个市场上的衰落损失将发生在不同的时期,这等于缓和了每一个市场上的衰落程度。事实上,这种效果也会延伸到其他几个相对意想不到的市场上,比如食糖。像黄金和白银一样,食糖市场在2006年5月中旬至6月中旬的20天内也发生了严重的衰落。因此交易调整不可取,因为它低估了中长期系统在实际交易中的衰落水平。
1987年的股崩也是这种现象的一个例子。在欧洲美元大幅跳空高开的那一天,许多平常并不相关的市场也一起剧烈跳空,令我损失惨重。进行交易调整的蒙特卡洛检验容易淡化这种非常现实的事件,因为它会将交易日期分散化,以至于它们的不利变化不会再发生在同一天。
许多有蒙特卡洛检验功能的软件可以用净值曲线调整法生成新的曲线,但它们没有考虑到另外一个重要的问题。根据我的测试和实践经验,我发现大趋势末端的衰落时间和程度远不是随机模拟结果可以比拟的。在这些大衰落期间,趋势跟踪系统的净值曲线呈现出序列相关性——也就是说,今天的资产变化与前一天的资产变化是相互关联的。更简单地说,坏日子往往集中出现,接踵而来,这并不是随机性事件的特征。
仍以2006年春季的黄金、白银和食糖市场为例,如果你调整的仅仅是资产净值的每日变化,那么从5月中旬到6月中旬的一连串剧烈变化将会消失,因为如果你只是随机性地从概率分布曲线甚至是真正的净值曲线中抽取数据,这样的巨变不太可能集中爆发。
考虑到这个问题,我们公司的模拟软件在调整净值曲线的时候也允许随机截取多个交易日的整段曲线,而不仅仅是单个交易日的数据。这样,模拟净值曲线就会把集中而来的不利变化保留下来,如实反映实际交易中的状况。我在测试中采用了截取20日整段曲线的调整方法,我发现,这种方法可以把净值曲线的自动序列关联保留下来,让模拟结果更具现实预测价值。
别样净值曲线
当我们用蒙特卡洛检验模拟出了别样净值曲线时,我们如何利用它们呢?事实上,我们可以用这些新曲线为某一个特定指标建立业绩分布图。假如未来的情况与我们在模拟中生成的别样景象有任何相似之处,那么未来的业绩潜力就反映在了这个分布图中。图12-3就是这样一个分布图。我们模拟生成了2000条别样净值曲线,计算了每一条曲线的RAR,然后在图上画出了结果的分布状况。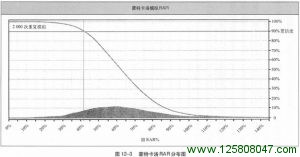
图中可见,有一条垂直线在图形上部穿越了曲线,它所对应的RAR就是置信度90%的RAR值:也就是说,所有模拟曲线中有90%的RAR高于这个值。对本例来说,2000次模拟中有90%得出了大于42%的RAR。
像这样的图非常有用,因为你可以从中认识到未来不可确知,有很多种可能性。不过你也不要过于深究这类报告的细技末节。不要忘了,这些数据来自于模拟的净值曲线,而净值曲线以历史数据为基础,自然摆脱不了第十一章所说的所有那些潜在缺陷。如果最初的测试就很糟糕,蒙特卡洛检验也不会是救世主,因为它本身就源自于最初的测试,不可能超然于原始数据之上。如果最优化矛盾导致RAR被高估了20%,那么蒙特卡洛检验所模拟出的别样净值曲线同样会将RAR高估20%,因为它使用的是同样的最优化参数值。
综上所述可知,历史测试充其量只是对未来趋势的粗略估计。稳健指标对未来表现的预测价值要高于较为敏感的指标,但仍然谈不上精确。如果某个人号称你的回报一定能达到某种水平,这个人要么在撒谎,要么根本是个外行;假如这人正在向你推销某样东西,我强烈怀疑他属于前一种情况。
下一章将介绍一些保护性的交易方法。使用这些方法,你的交易会更加稳健,也就是说,你不再那么容易遭受大起大落之苦。
 峰汇在线
峰汇在线




