骗子们还会用其他方法来制造不切实际的历史检验结果。最胆大妄为的那些人会有意使用过度拟合或曲线拟合来美化他们的系统。人们常常将过度拟合与最优化矛盾混为一谈,但实际上它们不是一回事。
过度拟合通常发生在系统变得过于复杂的时候。有时候,你可以通过添加法则来提高一个系统的历史表现,但这仅仅是因为这些怯则影响了屈指可数的几笔重要交易。添加法则会导致过度拟合,这对发生在关键时期的交易来说尤其明显。比如,假如一条法则要求你在接近最高峰的时候退出一个特别大的赢利头寸,这当然会提高你的系统表现,但如果这条战则对其他情况没有充分的适用性,这就成了过度拟合。
我曾见过许多系统兜售者在一段相对低迷的时期后用这种手段来提高他们的系统表现。他们有时候会把修改过的系统称为原版系统的“加强版”或“二代”。如果你想购买这一类的“加强”系统,你应该好好研究一下那些新添加的陆则,确保那些改进不是过度拟合的结果。
我发现用极端的例子来说明一种现象往往有助于我们更好地理解它。所以,我想给出一个极端过度拟合的例子。我会从非常简单的双重移动均线系统开始,然后添加一些法则,开始数据的过度拟合。
我们知道,这个系统在最后6个月的测试期内遭受了一次非常严重的衰落。所以,我会加入几条新法则,通过解决衰落问题来提高系统的表现。当衰落幅度达到一定的水平时,我就把我的头寸规模降低到一定的百分比自在衰落期结束后,我再把头寸恢复到正常水平。
让我们把这条新法则添加到系统中。这个法则有两个需要最优化的参数:一是头寸压缩的百分比,二是开始头寸压缩的衰落限制标准。根据模拟出的净值曲线,我决定在衰落幅度达到38%的情况下把头寸减小90%。添加这条战则大大提高了系统的表现,回报率从没有这条徨则时的41.4%上升到了45.7%,最大衰落从56%下降到了39.2%,MAR比率从0.74上升到了1.17。你可能会想:“这是个很棒的故则,系统大有改善。”事实上,你完全错了!
问题在于,这个法则在整个测试期内只有这一次发挥作用。它发生在测试期马上就要结束的时候,而我加入这条怯则是因为我已经知道了净值曲线的形状。因此,系统已经被有意地进行了数据拟合。“这有什么大不了的?”你可能会问。那就让我们看看图11-6,也就是不同衰落限制下的MAR比率。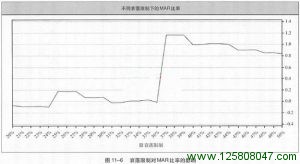
很明显,当我们把衰落限制下降到37%以下时,系统的表现急转直下。事实上,衰落限制只下调了1%,系统就从每年赢利45.7%陡然变为每年亏损0.4%。原因何在?原来,下调衰落限制后,这个法则将在1996年8月间生效,导致我们把头寸规模大幅削减,以至于后期赢利太少,没能从衰落中恢复元气。由此可见,这条怯则并没有那么好。它在第一次试验中有效仅仅是因为那次衰落发生在测试期即将结束的时候,头寸削减对后期表现的影响并没有体现出来。
参数值的微小变化却引发了交易结果的剧烈变化,这种现象被交易者们称为峭壁(cliff)。峭壁的出现是个很好的信号,这证明你可能已经犯了过度拟合的错误,而且你的实际交易结果可能会与测试中的结果大相径庭。峭壁现象也是我们认为参数最优化有益的原因之一:通过最优化程序,你可以发现峭壁,在开始交易之前就修正这个问题。
样本规模的统计学价值
正如我们在第二章中所说,人们往往对某种特定现象的少数事例过于重视,但却忽略了一个重要事实:从统计学上说,我们从寥寥几个例子中得不出太多的结论。这个问题就是过度拟合的主要缘由。添加某些不太经常发挥作用的法则会导致无意中的过度拟合,而这会造成事后测试结果与实际交易结果的差异。
这个问题经常在不经意间发生,因为大多数人都不会从这样的角度考虑问题。季节性因素就是个很好的例子。如果你想用10年的数据来分析某个特定的季节性现象,你最多只有10个例子可用,因为你的测试期只有10年。这样的样本规模没有什么统计学价值,因此任何以这些数据为依据的测试都对未来的表现没有太多的借鉴意义。
假设我们忽略了这个问题,想让电脑帮我们找到一个数据拟合的完美方在去。你可能发现有好几年的9月份都表现不佳,于是你想加入一条法则,在每年的9月份都将头寸削减到一定的比例。由于你有电脑,你可能想借助电脑模拟来找出所有的季节性逆境时期,每到这样的时期,你就会削减你的头寸。
我把这样的方法用在了本章所说的系统中。我进行了4000次测试,看了看季节性调整的效果:从每个月的月初开始削减头寸,在特定的天数内削减一定的百分比,然后在特定天数之后将头寸恢复到最初的规模。结果,我在10年的测试期内发现了两个可调整的时期。如果在每年9月份的头两天以及每年7月份的头25天内都将头寸规模降低96%,则系统的表现会提高,提高多少呢?
加入这条法则后,回报率进一步从45.7%上升到58.2%;衰落幅度略有提高,从39.2%变为39.4%;MAR比率则从1.17提高到1.48。乍一看,我们还是会认为:“这是个很棒的法则,系统大有改善。”
遗憾的是,这条陆则生效仅仅是因为在过去的这两个季节性时期发生过严重的衰落,并不是因为这两个时期有什么神奇之处。未来的同样时期内再发生同样衰落的可能性并不大。这就是最糟糕的那种过度拟合,但你想不到有多少聪明人曾落入这样的陷阱。
如果不知情,你可能会以为这个系统非常好,可以用来交易了。你甚至可能向朋友和家人们吹嘘这个绝妙的系统,想从他们那里筹一笔钱。问题是,这个系统的实际回报率只有41.4%,不是58.2%;衰在是56.0%,不是39.4%;MAR比率是0.74,不是1.48。系统的实际表现注定会令你大失所望,因为你已经被曲线拟合手段下的美好景象迷惑了。
接下来,我会谈谈如何避免本章中所提到的这些问题。我会告诉你如何为了将交易者效应的影响最小化而判断一个系统真正的潜在效果,如何现别随机效应,如何正确地最优化,以及如何避免对历史数据的过度拟合。
 峰汇在线
峰汇在线




