在系统测试中,你要做的是观测相对表现,分析未来潜力,判定一个特定理念是否有价值。但这里面有个问题,那就是公认的那些业绩衡量指标并不是非常稳定,也就是说,它们不够稳健。这就使评判一个理念的相对优势变得非常困难,因为寥寥几次交易中的微小变化就能对这些不稳健指标的值产生巨大的影响。指标的不稳定性可能导致测试者过高地评价一个理念,或是盲目地抛弃一个本来很有潜力的理念——因为它受到了不稳定指标的影响,并没有展现出应有的潜力。
如果对数据稍作改变并不会显著影响一个统计指标,我们就说这个指标是稳健的。但现有的指标对数据的变化都太过敏感,因此都太不稳健。正因为如此,在我们对交易系统作历史模拟检验时,参数值的轻微变化就会带来某些指标值的大幅变化。这些指标本身就是不稳健的——也就是说,它们对数据的轻微变化太过敏感。任何对数据有影响的因素都会对测试结果产生过大的影响,这很容易导致数据拟合,很容易让你被不切实际的测试结果所迷惑。要想有效地测试海龟方棒,我们要做的第一件事就是克服这个问题,找到稳健的业绩衡量指标。
在我最初参加海龟计划的面试时,比尔·埃克哈特就曾问过我这样一个问题:“你知道什么是稳健的统计指标吗?”当时我茫然地呆坐了几秒钟,然后坦白说:“我不知道。”现在我可以回答这个问题了。事实上,数学中有个专门研究不完全信息和错误假设的分支就叫作稳健统计学(robust statistics)。
从这个问题中明显可以看出,比尔对测试和历史数据研究的不完善本质有清醒的认识,对不确定性也颇有研究,这不仅在当时难能可贵,在今天依然如此。我相信这正是比尔能获得那种傲人业绩的原因之一。
这也又一次证明了里奇和比尔的研究和思维是多么超前于那个时代。我学到的越多,对他们对这个领域的贡献就越发敬畏。但我也惊讶地发现,相比起里奇和比尔在1983年的认识,现在的交易行业并没有太大的进步。
前面的章节把MAR比率、CAGR(平均复合增长率)和夏普比率用作相对表现的衡量指标。但这些指标并不稳健,因为它们对测试期的起始日和终止日非常敏感。这对短于10年的测试来说尤其明显。让我们看看将一次测试的起始日和终止日调整几个月会怎么样。假设我们从1996年2月1日而不是1月1日开始测试,一直测试到2006年4月30日而不是6月30日。也就是说,我们去掉了最初的一个月和最后的两个月。
在最初的测试期内,三重移动均线系统的测试得出了43.2%的回报率、1.39的MAR比率和1.25的夏普比率。但在修改了起止日后,回报率上升到了46.2%,MAR比率提高到了1.61,夏昔比率也提高到了1.37。ATR通道突破系统的最初测试结果是回报率51.7%,MAR比率1.31,夏昔比率1.39。起止日调整后,回报率攀升到了54.9%,MAR比率上升到了1.49,夏普比率提高到了1.47。
这三个指标之所以都这样敏感,是因为回报率指标对测试期的起止日非常敏感,而回报率又是MAR比率和夏普比率的要素(对MAR比率来说是CAGR,对夏昔比率来说是月度平均回报率)。如果衰落发生在测试期的开端或结尾附近,最大衰落这个指标也会对测试期的起止日高度敏感。这会把MAR比率变得特别敏感,因为它的分子和分母部分都对测试起止日敏感,变化的效果也就在计算中成倍放大了。
CAGR之所以对测试起止日敏感,是因为它在对数刻度图中就等于曲线起点和终点的连接线的斜率,而改变起止日会令这条直线的斜率大大改变。我们可以从图12-1中看到这种效果。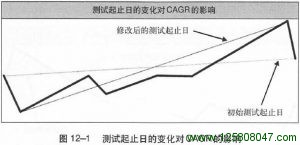
如图,标有“修改后的测试起止日”的直线斜率高于标有“初始测试起止日”的直线。在最初的测试中,1996年1月间发生了一次衰落,2006年五六月又发生了一次。因此,我们在把测试期掐头去尾之后,也就去除了这两次衰落。这在图12-1中看得很清楚:把前后两端的衰落去掉后,代表CAGR的连线斜率大大提高了。
 峰汇在线
峰汇在线




