11 次要的斐波纳契数-外汇理论书籍-峰汇在线

还有与斐波纳契数列相关的几个其他数字，这几个数字同样具有“和谐”的特性。尽管源自斐波纳契数列的许多数字都可以运用于这一方法之中，但是，本书并未将全部的数字包括进来。下面所提供的数字才是确定和谐形态的最重要的那部分。
0.382，0.500，1.000，2.000，2.240，2.618，3.140
要重点强调的是，这些数字应该发挥其他主要的斐波纳契数字和清晰的价格形态对潜在逆转区域的补充作用。在估量价格行为时，尽管这些数字并不像主要的斐波纳契数字那样至关重要，但它们也是很有效的数字。应该注意到这些数字存在的重要性。本书展示的很多简单的投射插图例子，将有助于用肉眼像识别主要的数字那样来辨别这些次要数字的训练。在下一节里，会有几个展示次要数字的有效用法的例子，特别是这些数字在复杂的形态中的运用。
尽管在确定和谐形态的分析中，这些数字很重要，但是，建议只将本章节作为一个基本部分来参考阅读。你可以浏览一下插图和图表的例子，来熟悉这些数字。

极端数字：2.240 ，2.618 ，3.140

当价格行为超过了 1.618 投射点时，这些数字就派得上用场了。当价格突破了 1.618 投射点的位置时，通常的价格行为是不稳定的。从这些数字所在价位产生的逆转行情可能是相当地剧烈，在价格触及到一个极端数字对应的价格之后，价格趋势会迅速产生逆转。在研究下面的图表的例子时，重点关注的是 1.618 投射点所在的区域。每一个实例中的价格行为的某些警告信号都逗留在主要的趋势中。然而，股票价格在极端投射点逆转时所形成的 K 线柱，它表明了主要的趋势正在改变。但是，这些数字最重要的一面是它们代表了股价的极端性质。

看涨极端数字

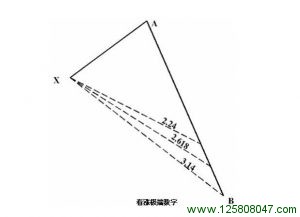
当一只股票的价格下降超过 1.618 投射点，极端的数字所在的区域是检验潜在逆转点的极好区域。2.240 比率大概是看涨极端数字中最为重要的一个，其次是 2.618，极其少见的是 3.140。事实上，3.140是一个终结点，在一定程度上，逆转通常会在这里发生。
如果一只股票价格测试到这些极限投射点，价格通常会突破 1.618 投射点。如果一只股票的价格在这个区域下跌，价格行为在这里通常是极端的并伴随着警告信号。然而，这些极端数字所在点位的价格逆转通常都是非常剧烈的。
下面的图表例子，演示了这些极端数字。这些图表是每种投射点基本框架的学习和参考的重点。

看跌极端数字

在价格上升超过 1.618 投射时，看跌极端数字是非常有效的。重要的是在极端价格超过这个区域时要做好准备。价格逆转可能相当激烈而且价格行为也是极其地动荡的。

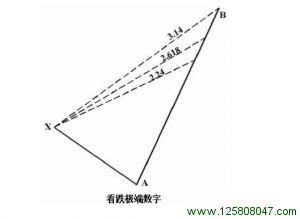
价格突破 1.618 投射点之后，重要的是要充分意识到这次的极限投射点，就像一个潜在逆转区域。2.240 大概是最具补充性质的一个逆转点。2.618 和 3.140 投射点也是这样可能发生逆转的点位，但不是经常地发生。
下面的例子描述了这些极限投射点。简略地浏览一下这些极限投射的例子，以使自己熟悉这些极限投射。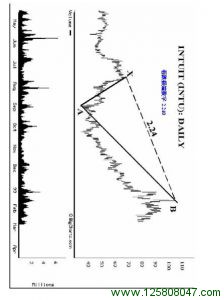

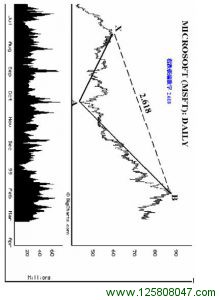
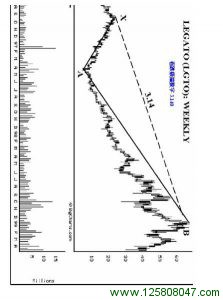
急剧的0.382回撤：

0.382 是一次剧烈的价格运动之后的急剧回抽或者回撤。在价格经过一段极端的运动之时，通常出现 0.382 回撤。0.382 回撤快速和突然的特性经常导致在同一个方向上的另一波极端价格运动。
通常，一波价格运动的 0.382 回撤，紧随其后的是 1.618 回撤。这意味着，如果 0.382 回撤等于 1，那么接下来的价格运动至少是 1.618 投射点。有时候，在非常极端的价格行为出现之后，随后的价格运动可能是 2.240，2.618 或 3.140 的回撤行为。最重要的概念是 0.382 与极端的价格行为紧密相连。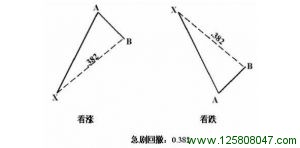
下面的例子说明了 0.382 回撤的特性。值得注意的是 0.382 回撤逆转之后的价格后行为通常是相当强劲的。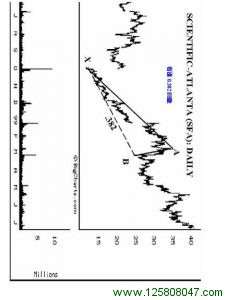

常量数字：0.500 ，1.000 ，2.000

把这些数字看作常量值的原因是因为他们不是直接来自斐波纳契序列，所以将其归为其他次要数字之列。这些数字频繁地在股票图表中出现。例如，一个双头或双底形态具有两个相等的价格波段。另一常见的是 50%回撤例子。通常，价格行为将回撤一段价格运动幅度的一半或者 0.5。这种情况很容易解读。事实上，就斐波纳契比率而言，大多数的技术分析人员都在使用这些数字。
就这些常量数字来说，本书没有提供任何的佐证例子，因为这种价格波段能够显而易见地识别出来。尽管这些数字可以有助于估量价格行为，但不要将他们当作是和谐数字。因而，仅将它们用来辅助一个潜在形态的补充分析。