斐波纳奇序列数字是十三世纪的意大利数学家,来自比萨城(Pisa)的里昂纳多·斐波纳奇 发现的(确切地说是重新发现的)。我们将概述这位奇才的历史背景,然后比较完整地讨论 以他的名字命名的序列(从技术上讲,它是 序列,而不是级数)数字。艾略特在撰写《自然法则》时,曾经解释说斐波纳奇序列数字提 供了波浪理论的数学基础。(对于波浪理论背后的数学的进一步讨论,请见沃尔特·E·怀特 (Walter E White)撰写的“波浪理论的数学基础(Mathematical Basis of Wave Theory)”,此文收录在了经典文库即将出版的一本书中。) 来自比萨城的里昂纳多·斐波纳奇 黑暗时代(Dark Ages)是欧洲文化几乎全面衰退的时期。它从公元476年罗屿帝围的衰亡,直至大约公元10 00年时中世纪(Middle Ages) 的开始。在这一时期,数学和哲学在欧洲日渐衰败,但在印度和阿拉伯却得到了充 分的发展,因为黑暗时代没有蔓延到东方。当欧洲逐渐从停滞不前中恢复过来的时候,地 中海发展成了条文化交流之河,指引来自印度和阿拉伯的商业、数学以及其他新思想流 人欧洲。 在中世纪早期,比萨城发展成了一个城墙坚固的城邦(City state)和繁荣的商业中心,它的滨水区反映了那时的商业革命(Commercial Revolution)。皮革、毛皮、棉花、羊毛、铁、铜、锡和香料都在比萨城内进行交易,而黄金允 当一种重要的货币。港口挤满了大到四百吨而且长至八十英尺的船只。比萨城的经济支 撑了皮革业和造船业,以及一家炼铁厂。即使按今天的标准来衡量,比萨城的政治体制也 足结构完善的。例如,共和国的自席治安官(Chief Magistrate)在任期内是得不到报酬的,在任期结束时,他的行政管理还可能会受到调查, 以决定他是否能拿到工资。事实上,我们的主人公斐波纳奇也是检查员之一。 生于1170至1180年的斐波纳奇,很可能生活在比萨众多塔楼中的一座里,他是一位杰出 的商人兼市政官的儿子。塔楼可以当作工厂、碉堡和家庭住宅,它的建筑结构可以使箭从狭窄的窗户里射出,并使烧开的柏油倒向接近塔楼的图谋不轨的陌生人。斐波纳奇活着 的时候,著名的比萨斜塔的钟塔尚在建造之中。它是当时比萨城打算建造的三座宏伟建 筑物中的最后一座,因为比萨大教堂和比萨洗礼堂早在几年前就完工了。
还是个学生的时候,斐波纳奇就开始熟悉当时的海关和商业实践,包括使用算盘,这曾在 欧洲作为一种商用计算器广泛使用。尽管斐波纳奇的母语是意大利语,但他还学会了其 他几种语言,包括法语、希腊语,甚至还有他熟练的拉丁语。
不久,里昂纳多的父亲就被派往北非的贝贾亚。任海关官员,他要求里昂纳多一同前往, 以完成学业。里昂纳多开始绕着地中海进行了许多商务旅行。在一次埃及之旅后,他出版 了他的名著《计算的书(Liber Abacci)》,这本书把有史以来最伟大的数学发现—— 十进制—— 介绍到了欧洲,十进制数字符号的首位数是零这种包括常见的符号0,1,2,3,4,5,6,7, 8和9的数学进制,就是今天人们广泛使用的所谓印度— 阿拉伯(Hindu—Arabic)进制。 在真正的数位制或位值制中,用任何与其他符号排列在起的符号表示的实际值,不仅取 决于它基本数字的值,还取决于这些基本数字在排列中的位置,例如,58的值与85的值不 同。尽管早在几千年前,巴比伦人和中美洲的玛亚人就已经分别建立了数位的或位值的 命数法,但他们的方法在其他方面十分笨拙。因此,首先采用零和位值的巴比伦进制,并 未被转记到希腊的甚至罗马的数学进制中,罗马命数法包括七个符号:I,V ,X ,L,C,D和 M,这些符号没有数字值。用这些非数字符号的进制进行加、减、乘、除运算,并不是件容 易的事,尤其是在数字较大的时候。矛盾的是,为了克服这些困难,罗马人使用算盘这种 古老的数字设备。因为这种设备是基于数字的,并含有零原理,所以它对罗马人的计算体 系起到了必要的补充作用。在那个时代,簿记员和商人都靠它来协助自己的工作。在《计 算的书》中解释了算盘的基本原理后,斐波纳奇开始在旅行中使用他的新进制。通过他的努力,这种计算方法简单的新进制最终传 入了欧洲。渐渐地,罗马数字被阿拉伯数字所取代。将这种新进制引入欧洲,是七百年前 罗马帝国衰亡后数学领域里的最重要的成就。斐波纳奇不仅使中世纪的数学保持了生气 ,而且还为更高等的数学领域,以及物理学、天文学和工程学的相关领域的巨大发展奠定 了基础。
尽管后来的世界几乎忘却了斐波纳奇,但他无疑是他那个时代的伟人。斐波纳奇的名声 是如此之大,以致于本身也是一位科学家和学者的弗里德里克二世(Frederic Ⅱ)为了寻找他,特别安排去比萨城访问。弗里德里克二世是圣罗马帝国的皇帝,西西里 王国和耶路撒冷王国的国王,欧洲和西西里王国二个贵族家庭的后裔,而且是那个时期 最有力的统治者。弗里德里克二世的观念与那些绝对统治者的一样,他将自己置身于一 个罗马皇帝应有的全部盛大场面之中。 斐波纳奇与弗里德里克二世的会见发生在公元1225年,这是当时比萨城的一件圣事。皇 帝一马当先,带领着由号兵、侍臣、骑士、官员和一大群野兽组成的长长的队伍。皇帝在 这位举世闻名的数学家面前提出的一些问题在《计算的书》中有详尽的记载。斐波纳奇显 然是解决了皇帝提出的问题,后来皇帝在宫廷热烈欢迎了他。公元1228年,当斐波纳奇修 订《计算的书》时,他把修订版题献给了弗里德里克二世。
斐波纳奇是中世纪最伟大的数学家,这样说太保守了。斐波纳奇总共有三本重要的数学 著作:1202年出版.并于1228年修订的《计算的书》.1220年出版的《实用几何学(Practica Geometriae)》,以及《求积法(Liber Quadratorum)》。公元1240年,钦佩他的比萨共和国的公民们把他记载成一位“言行谨慎, 学识渊博的人”,《大英百科全书》的资深编辑约瑟夫·基斯最近曾说,未来的学者迟早会“ 公正地对待比萨的伦纳德,他是世界上伟大的学术先驱之一”,多年后.斐波纳奇的著作才从拉丁文译成英文。对于那些感兴趣的读者,约瑟夫基斯与弗朗西斯·基斯(Frances Gies)和著的“比萨的伦纳德以及中世纪的新数学 (Leonard of Pisa and the New Mathematics of the Middlc Age)”足一篇关于斐波纳奇时代及其著作的杰出论文。
尽管斐波纳奇是中世纪最伟大的数学家,但他的纪念物仅是一座与比萨斜塔隔着阿诺河( Arno River)的雕像,以及两条以他的名宁命名的街道—— 一条在比萨市,另一条在佛罗伦萨市。奇怪的是,在参观179英尺高,垂直方向倾斜17英尺 的比萨斜塔的游客中很少有人听说过斐波纳奇,或是瞻仰过他的雕像。斐波纳奇与公元1 174年开始建造的比萨斜塔的设计师波纳纳(Bonanna)是同时代的人。二者都对世界做出 了贡献,但是一个影响远远超过另一个的人却是那么不为人知。 斐波纳奇序列 在《计算的书》中提出的一个数学问题产生了数字序列1,1,2,3,5,8,13,2l,34,55,89, 144,如此无穷,这就是今天所知的斐波纳奇序列。这个问题是: 如果一对兔子从第二个月开始,每个月生一对新的兔子,而且不发生死亡,那么一对兔子 在一年内总共会产生多少只兔子? 为了得到答案,我们发现每一对兔子,包括第一对,需要一个月的时间成熟,它们一 旦可以生育,则每个月都会生出一对新兔子。在开始的头两个月的每一个月中,兔子的对 数是一样的,所以序列是1,1。第一对兔子最终在第二个月使兔子的数量翻番,所以在第 三个月开始时,就有了两对兔子。在这两对兔子中,老兔子在接下去的一个月里又生了一 对新的兔子,这样就有了三对兔子,所以在第四个月的开头,序列扩大到了1,1,2,3。在 这三对兔子中,两对老兔子,而不是那对最年轻的兔子,又可以生出新兔子,这样兔子就 扩大到了五对。在下一个月里,有三对可以生育,所以序列扩大到了1,1,2,3,5,8,依此 类推。图3— 1是以对数加速度膨胀的兔子家族树。让序列这样发展几年,就会产生天文数字。比如,10 0个月后,我们就会得到354,224,848,179,261,915,075对兔子。由兔子问题产生的斐波纳奇 序列有着许多有趣的特性,而且反映出序列中的各项几乎有着恒定的关系。 序列中任何两个相邻的数字之和形成了序列中的下一个更大的数字,即,1加1等于2 ,1加2等于3,2加3等于5,3加5等于8等等,至无穷。
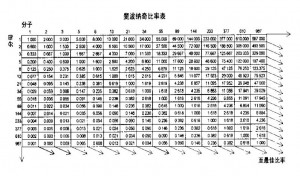
黄金比率 在序列中的前几个数字以后,任何一个数字与下一个数字之比大约是0.618比1,而与前一 个数字之比大约是1.618比1。数字在序列中越靠后,比值越接近φ子,φ是无理数0.618034 。序列中间隔一个数字的相邻的两个数字的比值是0.381,其倒数是2.618。图3— 2是链接所有1至144的斐波纳奇数字的比率表。
φ是唯一一个与1相加,可以得到其倒数的数字:0.618+1=1÷0.618。把相加和相乘结合,可 得到以下等式序列:  除了1和2之外,任何斐波纳奇数字乘以4,再有选择地加上一个斐波纳奇数字,可以得到 另一个斐波纳奇数字,因此:
除了1和2之外,任何斐波纳奇数字乘以4,再有选择地加上一个斐波纳奇数字,可以得到 另一个斐波纳奇数字,因此:
3×4=12 ; +1=13.
5×4=20 ; +1=21.
8×4=32 ; +2=34,
13×4=52 ;+3=55,
21×4=84 ;+5=89,
依此类推。、 在新序列发展的时候,第二三个序列从与4倍的乘积相加的数字开始。这种关系是可 能的,因为隔两个数字相邻的斐波纳奇数字的比值是4.236,这里0.236不仅是4.236的倒数 ,也是4.236与4的差。其他乘积可以产生不同的序列,这些序列都是基于斐波纳奇乘积。
以下,我们例举了部分与斐波纳奇序列有关的现象:
1.两个连续的斐波纳奇数字没有公约数。
2.我们发现,如果把斐波纳奇序列标上序列号1,2,3,4,5,6,7,等等,除了第、第二 和第四个斐波纳奇序列数字以外,每次遇到素数(仅能被l及其自身整除的数)的斐波纳奇 数字时,它的序列号也是素数。相似地,从斐波纳奇序列数字的第六项开始。所有合数(除 了1及其自身以外,还能被其他整数整除的数)的序列数都表示着合数的斐波纳奇数字,如 下表。但反过来,这种现象就不 成立了。
3.序列中的任何十个数字之和,均可被11整除。
4.序列中发展至任何一步的所有的斐波纳奇数字之和加上1等于与最后一个加数向后相 隔一项的斐波纳奇数字。 5.从第一个1开始的任何相连的斐波纳奇序列数字的平方和,等于被选的最后一个序列 数字乘以这个数字之后的斐波纳奇序列数字。
6.一个斐波纳奇数字的平方,减去序列中 与这个数字向前相隔一项数字的平方,结果还是一个斐波纳奇数字。 7.任何斐波纳奇数字的平方等于序列中这个数字的前一项与后一项的乘积,再加上1或 减去1。在整个序列中加上1或减去1相互交替。
8.一个斐波纳奇数字Fn的平方乘以下一个斐波纳奇数字Fn+1 的平方等于斐波纳奇数 字F2n+1 。公式Fn2+Fn+12=F2n+1适用于直角三角形,直角三角形二直角边的平方和等于斜边 的平方。
9.有一个公式可以表示数学中两个无处不在的无理数π和Φ之间的关系:F ≈100×π × n Φ(15- Φ) ,其中Φ=0.618……,n代表斐波纳奇序列中各项的序列号,而Fn则表示这个项本身。在 此情况下,数字“1”仅代表了一次,因此F ≈1,F ≈2,F ≈3 ,F ≈5,等等。 1 2 3 4
10.还有一个延伸思维的现象,据我们所知以前未曾提到过,即斐波纳奇数字问的比值非 常接近于另一个斐波纳奇数字的千分之一,其差值又是第三个斐波纳奇数字的干分之一 ,在序列中都是如此(见比率表,图3— 2)。因此,在比率上升的方向上,相同的斐波纳奇数字之比是1.00,或0.987加上0.013 ;相邻 的斐波纳奇数字之比是1.618,或1.597加上0.021 ;相隔一项的斐波纳奇数字之比是2.618, 或2.584加上0.034 ;依此类推。在比率下降的方向上,相邻的斐波纳奇数字之比是0.618,或 0.610加上0.008 ;相隔一项的斐波纳奇数字之比是0.382,或0.377加上0.005 ;相隔二项的斐 波纳奇数字之比是0.2366,或0.233加上0.003 ;相隔三项的比率是0.146,或0.144加上0.002 ;相隔四项的比率是0.090,或0.089加上0.001 ;相隔五项的比率是0.056,或0.055加上0.001 ;相隔六项至相隔十二项的比率本身就是从0. 034开始的,一个斐波纳奇数字的千分之几。有趣的是,根据这种分析,相隔十三项的二个 斐波纳奇数字之比又回到了0.001,斐波纳奇序列数字开始的千分之一。在所有的计数中, 我们真的像斐波纳奇序列数字的崇拜者所说的那样,创造了“在一个无穷级数中繁衍”的“ 的”的特性。 特征传递”,揭示了“所有数学关系中最紧密
最后,我们注意到,(Error!5+1)/2=1.618而(Error!- 1)/2=0.618,其中Error!=2.236,5是波浪理论中的一个最重要的数字,而它的平方根是φ 的数学解。 1.618(或0.618)即所谓黄金比(Golden Ratio)或黄金平衡(Golden Mean)。它的比例令眼睛和耳朵感到和谐。它在生物、音乐、绘画和建筑中都有表现。威廉· 霍法(William Hoffet)在为1975年12月号的《史密森人(Smithsonian Magazine)》杂志撰写的文章中说: ……0.618034与1之比是纸牌与巴台农神庙(Parthenon)、向日葵与蜗牛壳、希 腊花瓶与外宇宙的螺旋星系的形状的数学基础。希腊人将他们的大量绘画和建 筑基于这个比例。他们称其为 “黄金平衡”。
斐波纳奇的魔术兔子,在许多意外的的地方出现。兔子的对数无疑是一种神秘 的自然的和谐,这种和谐宜人、悦目、甚至动听。比如,音乐的一度有八个音 符。在钢琴上它用8个白键,5个黑键表示—— 共13个键。最悦耳动听的音乐是大六度绝不是巧合。音符E的振动是音符C的0.6 2500倍。音符A仅仅与黄金平衡相差0.006966,大六度的比率引起内耳耳蜗—— 正好也是呈对数螺线的形状的器官——的和谐振动。
斐波纳奇数字和黄金螺线在自然界中的不断出现,精确地解释了为什么0.61803 4与1之比在绘画中让人感觉如此舒服。人们可以在绘画中发现基于黄金平衡的 生命肖像。 小到原子结构、大脑中的微细管以及DNA分子(见图3— 9),大到行星的距离和周期,大自然在其最本质的积木和最高级模式中采用黄金比,它包 含在非常广泛的现象中,如准晶体排列,光束在玻璃表面上的反射,大脑和神经系统,乐 曲改编,植物和动物的结构。科学正在迅速证明有一种基本的自然比例构造原理。顺便说 一下,你用你五个附肢中的两个拿着这本书,每个附肢有二三个相连的部位,附肢的顶端 有5个手指或脚趾,而每个手指或脚趾必有3个相连的部分,这是个或许可以说明波浪理 论的5-3-5-3的行进。
黄金分割
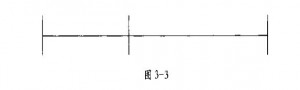
较短的部分与较长的部分之比,等十较长的部分与整个长度之比(见图3— 3),任何长度都可以这样分割。这个比值永远是0.618。
 黄金分割出现在整个自然界。事实上,人体各处——从外形尺寸到面部器官的位置— —都是一幅体现黄金分割(见图3— 9)的织锦。“柏拉图在他的《蒂迈欧篇(Timaeus)》中”彼得·汤普金斯(Peter Tompkins)说,“曾深入考虑过φ及其产生的黄金分割比例关系—— 所有数学关系中最紧密的约束,把它当作宇宙中物理学的关键。”十六世纪,约翰尼斯·开 普勒在谈到黄金分割或称“神赐分割”时,说它实质上描绘了万物,尤其象征了“特征传递” 的上帝的造化。人体可以在肚脐处分成黄金分割。统计上的平均值正好是0.618。这个比率 对男女分别成立,是一种“特征传递”的造化的完美标志。人类全部的行进也是一种“特征 传递”的造化吗?
黄金分割出现在整个自然界。事实上,人体各处——从外形尺寸到面部器官的位置— —都是一幅体现黄金分割(见图3— 9)的织锦。“柏拉图在他的《蒂迈欧篇(Timaeus)》中”彼得·汤普金斯(Peter Tompkins)说,“曾深入考虑过φ及其产生的黄金分割比例关系—— 所有数学关系中最紧密的约束,把它当作宇宙中物理学的关键。”十六世纪,约翰尼斯·开 普勒在谈到黄金分割或称“神赐分割”时,说它实质上描绘了万物,尤其象征了“特征传递” 的上帝的造化。人体可以在肚脐处分成黄金分割。统计上的平均值正好是0.618。这个比率 对男女分别成立,是一种“特征传递”的造化的完美标志。人类全部的行进也是一种“特征 传递”的造化吗?
黄金矩形
黄金矩形相邻两边之比是1.618比1。要构造一个黄金矩形,首先得画一个两个单位长 度乘两个单位长度的正方形,然后从一边的中点至对边直角的顶点作一条连线,如图3— 4。
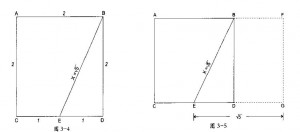
三角形EDB是一个直角三角形。大约在公元前550年,毕达哥拉斯曾证明,直角三角形的 2 2 2 2 斜边(X)的平方等于二直角边平方的和。因此,在本例中,X =2 +1 ,或X =5。所以线段EB 的长度必是5的平方根。构造黄金矩形的下一步是延长线段CD至点G,使EG的长度等于5 个单位长度的平方根,或2.236个单位长度,如图3— 5所示。画完时,矩形相邻两条边呈黄金比,所以矩形AFGC和矩形BFGD都是黄金矩形。 证明过程如下: 
因为矩形的两条邻边呈黄金比.所以根据定义,这个矩形是黄金矩形。 黄金矩形的知识极大地美化了艺术作品。在古埃及、古希腊和文艺复兴(Reaissance)这 些文化高峰时期,黄金比的价值与应用的魅力尤其强烈。里昂纳多·达·芬奇曾为黄金比率 赋予了深远的意义。他还发现这种比率使人感觉舒服,并说,“如果件东西没有正确的外 表,它就没有用。”达·芬奇的许多绘画作品拥有正确的外表,因为他有意识地用黄金分割 来增强绘画的表现。古代的建筑师和现代的建筑师—— 最著名的是那些设计雅典巴台农神庙的建筑师,已经将黄金直角三角形成功地运用到了他们的设汁之中。 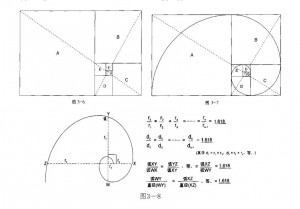
显然,Φ比率确实能够对形态的外观产生影响。试验人员已经证实这个比例有美感。例如 ,当要求被试验者从一组不同类型的矩形中选择一个矩形时,平均结果通常接近于黄金 矩形的形状。当要求被试验者以他们最喜欢的方式,将一根杆子与另一根杆子十字交叉 时,被试验者通常会用一根杆子子将另一根杆子划分成Φ比例。窗户、画框、建筑、书籍以 及墓地的十字架常常近似于黄金矩形。 就像使用黄金分割,黄金矩形的价值不仅仅限于美学,而且还有功能上的作用。在无数例 子中最有说服力的就是,DNA的双螺旋结构本身在它扭转的有规则的间隔处精确地创造 了黄金矩形(见图3—9)。 黄金分割与黄金矩形代表了自然和人工美学及功能的静态形态,而代表美学舒适的物力 论(Dynamism)—— 一种生长或发展的有序过程,就要用到宇宙中最独特的形态—— 黄金螺线。
黄金螺线 黄金矩形可以用来构造黄金螺线。任何黄金矩形,如图3— 5中的,都可以划分成一个正方形和一个小的黄金矩形,如图3— 6所示。这个过程理论上可以无限延续。我们这样做出的正方形明显向内旋转,它们被标 示成A 、B、C、D、E、F和G。 本身互为黄金比例的两条虚线,对角分割开了黄金矩形,并精确指出了旋转正方形的理 论中心。从靠近这个中心的地方,我们可以如图3— 7所示沿正方形增大的方向,通过用曲线连接每个旋转正方形的交叉点来绘制螺线。当正 方形向内或向外旋转时,它们的连接点就描绘出了一条黄金螺线。 在黄金螺线进化的任何一点,弧长与直径之比是1.618。黄金螺线的直径和半径依次与相 距90度的直径呈1.618的比率关系,如图3—8所示。 黄金螺线是对数螺线,或称等角螺线的一种类型,它没有边界,而且是形状恒定。从螺线 上的任何一点,螺线都可以向内向外无限推移。既遇不到中心,又碰不到终点。图3— 8中的对数螺线的核心,如果在显微镜下观察,与从几光年外看到的对数螺线外形一模一 样。 如果欧几里得几何形态(也许除了椭圆以外)意昧着静止,那么螺线就意味着运动:生长与 衰老,扩散与收敛,前进与后退。对数螺线是在整个宇宙中发现的自然生长现象的精华表 述。它覆盖了小到原子粒子,大到银河系的各种规模的运动。就像大卫·伯嘉米尼(David Bergamini)在撰写《数学(Machematics)》(“时代生活(Time- Life)” 出版的科学书库系列丛书中的一部)时指出的那样,彗星的尾巴从太阳开始画出了 一条对数螺线。圆蛛(Epeira)将它的蜘蛛网织成对数螺线。细菌生长的加速度可以用对数 螺线表示。陨晕在地球表面爆裂时,形成的陨坑与对数螺线相符。松果、海马、蜗牛壳、软 体动物的壳、海浪、蕨类植物、动物的角、以及向日葵和菊花上的种子分布曲线,都呈对 数螺线。旋风云、漩涡和外太空的星系以对数螺线旋转。甚至由互成黄金分割的三根骨头 组成人的手指,在弯曲时也与逐渐死亡的一品红的叶了(见图3— 9)的螺线形状一样。在图3— 9 中,我们可以在许多形态中看到这种宇宙影响的反映。无尽的时间和空间分开了松果和 螺旋的星系,但它们结构是一样的:1.618比率,也许它是主宰动态自然现象的基本规律。 因此,作为自然界的重大结构之,作为一种无穷扩散或收敛的力量,一种主宰动态过程的 静态规律,黄金螺线在我们面前以符号形式展开,所有这些都受1.618比率,即黄金平衡的 支撑。 φ的含义 各个时代的盖世奇才都深刻赏识这种普遍现象的价值。历史上有许多杰出学者痴迷这种 数学表达的例子。毕达哥拉斯选择五角星作为他的社团的符号,因为五角星中的每条线 段与小一级的线段呈黄金比;十七世纪著名的数学家雅科布·怕努利(Jacob Bemoulli)命令把黄金螺线蚀刻在了自己的墓碑上;伊萨克·牛顿(Isaac Newton)让人在他的床头板(现由位于美国新罕布什尔州新波士顿市的重力基仓会(Gravity Foundation)收藏)上刻上了相同的螺线。已知最早的黄金分割狂热爱好者的是埃及吉萨(Gi zeh)金字塔的建筑师,大约5000年前,他们就在建筑中记录了φ的知识。埃及的工程师们 有意识地将黄金比融入了大金字塔中,他们使大金字塔侧面的斜高等于底边长度一半的1 .618倍,这样塔高同时就是1.618的平方根乘 以底曲长度的一半,按《大金字塔的秘密(Secrets of the Great Pyramid)》(哈普&罗出版公司(Harper&Row),1971年)的作者彼得·汤普金斯的说法,“这个 关系表明希罗多德(Herodotus)的报告实际上是正确的,因为大金字塔塔高的平方是Error! ×Error!=φ,而斜面的面积是1×φ=φ”。此外,通过使用这些比例,埃及的设计师(显然是为 了建造北半球的比例模型)能以成熟的数学方法束使用π和φ,因此他们可以求圆的面积和 球的体积(也就是,使它们有相同的面积和相同的体积),这种技艺在随后的四千多年里未 被重复过。 如果仅仅提到大金字塔可能会引起怀疑(也许是出于更好的解释),但要注意,它的形态反 映出科学、数学、艺术和哲学思想的大师们也为之着迷,这些大师包括柏拉图、毕达哥拉 斯、开普勒、达·芬奇和牛顿,那些设计和建造金字塔的人也是才华横溢的科学家、天文学 家,数学家和工程师。很清楚,他们是要成千上万年地将黄金比率作为一种有至高无上价 值的东西保存。这些高超的学者从事这种任务本身就是十分重要的.希腊的和欧洲启蒙 运动时期的智者,出于对黄金比率的痴迷也加入了这些人的行列。至于为什么,我们只能 融汇一些作家的说法。这种融汇尽管笨拙但符合我们自己的观察。在大金字塔建成几个 世纪以后,人们猜想它是向那些证明自己适于理解宇宙奥秘的人传授知识的庙卞。这种“ 秘密”,也就是水恒的秩序和生长的复杂道理,只能教授给那些能够站在事物的外表之上 ,以认识万物究竟是什么的人。这种“秘密”包括φ吗?汤普金斯解释说,“舒瓦勒·卢比茨(Sc hwaller de Lubicz)认为埃及的法老认为φ不仅是一个数字,而且是一种创造机能或一个无穷级数重 现的象征。对于他们来说,它代表了‘生命之火、精子的雄性活动、圣约翰福音中据到的逻 各斯(Logos)’,赫拉克里特和后来的异教徒,以及犹太教和基督教的哲学家,将逻各斯这 个希腊词定义为意味着宇宙的理性秩序、一种内在的自然法则、一种蕴藏在万物中的给 与生命的力量,以及主宰并渗透世界的共同的结构力量。”
在阅读这些深奥而时髦的描述时,要考虑这些人不能清楚地看到他们感觉到的东西。他 们没有图表和波浪理论来使自然的生长模式清楚明了,而是尽己所能来描述一种他们认 为给自然界定形的组织原理。如果这些古代的哲人认为有一种共同的结构力量主宰并渗 透着世界的观点是正确的,那么它不会主宰并渗透到人类世界中吗?如果宇宙中的各种形 式,包括人体、大脑和DNA反映了φ的形态,那么人类的行为也反映这种形式吗?如果φ是 宇宙中的生长力量,它能在背后推动人类生产力的进步吗?如果φ是一种创造机能的象征 ,它会主宰人类的创造活动吗。如果人类的发展是基于“一种无穷级数”的生产与再生产, 那么有可能,甚至有理由为这种发展呈φ的螺线形态吗。而且在人类生产力的估价,也就 是股票市场的运动中,这种形态可以识别吗?聪明的埃及人显然知道在宇宙的无序外表之 后隐藏着有序和生长的真理。在20世纪80年代,现代的“混沌理论” 已经再次发现了这种想 法。相似地,我们认为,如果我们考察的是股票市场的本质,而不是一种基于草率考虑之 上的粗糙的市场表现,那么股票市场是可以被正确理解的。股票市场不是对即时消息随 机的、无形的大众反映,而是一种对人类进步的形态结构的精确记录。 请把这个概念同天文学家威廉·金斯兰德(William Kings- land)在其著作《实际与理论中的大金字塔(The Great Pyramid in Fact and in Theory)》中的话相比较,他写到,埃及的天文学/星象学是一种“与人类进化大循环相联 系的深奥科学。”波浪理论解释了人类进化的大循环,并揭示了它们怎样以及为什么要这 样展开的道理。而且,它不仅包含了小规模的循环,还包含了大规模的循环,这些循环都 是基于一种物力悖论。并在一种恒定形态中变化。 正是这种形态赋予了宇宙结构和统一。自然界中没有什么东西表叫生命是无序的或无形 的。“宇宙”一词意味着“一种秩序”。如果生命有形态,那么我们无法拒绝,作为生命现实 的一部分,人类进步也有秩序和形态的可能性。延伸开去,估价人类生产企业的股票市场
也有秩序和形态。所有了解股市的技术分析手段都是基于秩序和形态的基本原理。但是, 艾略特的理论更胜一等,它假设,形态无论是大是小,它的基本的结构是衡定的。 艾略特在他的第二项专题研究中,用《自然法则宇宙的奥秘》来代替《波浪理论》,并将自 然法则运用到各种人类活动中。艾略特说波浪理论是宇宙的奥秘可能有些过头了,因为 大自然看起来已经创造了数不清的形式和过程,而不仅仅只是一种简单的结构。然而,前 面提到过的历史上的一些科学臣匠,很可能会赞同艾略特的结论。至少,说波浪理论是宇 宙中最重要的奥秘之一是可信的。 股市螺线形发展中的斐波纳奇数学 我们能推论并观察到股市像许多自然现象那样按相同的数学基础运行了吗?回答是“是”。 正像艾略特在他最后的统一结论中解释的那样,各种波浪的行进有着相同的数学基础。 斐波纳奇序列主宰着在股票指数总体运动中形成的波浪数目,它按照我们在第一章开头 所说的5:30的内在关系展开。 正像我们首先在图1— 4 中表明的那样,市场的本质结构可以产生完整的斐波纳奇序列。一个调整浪最简单的表 现形式是直线下降。一个推动浪最简单的表现形式是直线上升。一个完整的循环是二条 直线。在下一级的复杂形态中,相应的数字是3、5和8。如图3— 10所示,这个序列可以无穷无尽。波浪产生斐波纳奇序列数字的事实说明,人类总体表达 出的情绪与这条数学自然定律相和谐。 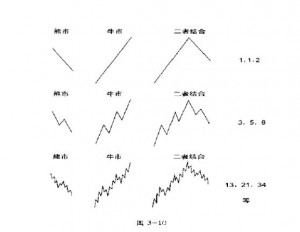
现在请比较图3一11和3— 12中出现的结构。每幅图都表示了内旋黄金螺线的自然法则,而且都受斐波纳奇比率的 控制。每一浪都与前一浪按0.618的比率相联系。事实上,DJIA点数的距离本身 就反映出斐波纳奇数学。在表示1930至1942年序列的图3— 11中,市场的摆动分别接近260点、160点、100点、60点和38点,这与下降的斐波纳奇比率 :2.618、1.618、l.000、0.618和0.382很相近。


在图3— 12中,从1977年的向上调整的浪X开始,指数的摆动几乎正好是55点(浪X) 、34点(浪(a)至 浪(c))、21点(浪(d)、13点(浪(e) 中的浪(a))和8点(浪(e) 中的浪(b)),即斐波纳奇序列数字本身 。从头至尾的净调整是13点,而且三角形端点正好处于930点的调整起始位置,这也是六 月份反弹的高点。无论你认为波浪中的实际点数是巧合还是结构的一部分,都应明白每 一个相连浪间0.618倍的比率常数不是巧合。第四章和第七章将重点讨论各种市场模式中 的斐波纳奇比率。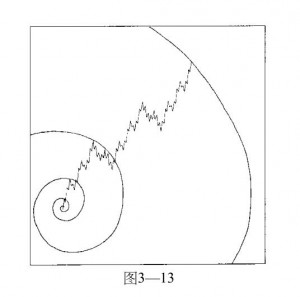
基于斐波纳奇序列的股市行为反映螺线形生长吗?回答再次是“是”。图1— 6表示的股市行进的理想艾略特概念是构造一条对数螺线的绝佳基础,图3— 13大致说明这一点。在这个构造中,每一个浪级更高的波浪的顶点都是与指数式展开的螺线的接触点。在这两种关键的途径中(斐波 纳奇序列和螺线形展开),对人类生产企业的社会估价反映出在整个自然界中发现的生长 形态。因此,我们得出结论,它们遵循相同的法则。 波浪理论结构中的斐波纳奇数学 即使是艾略特波浪形态有序的结构复杂性也反映出斐波纳奇序列。有1种基本形态:五浪 序列。有2种波浪方式:驱动浪(可以细分成波浪的基本级,用数字标示)和调整浪(可以细 分成波浪的辅助级,用字母标示)。有3 目波浪的简单模式:五浪、三浪和三角形(它既有五 浪的特征和又有三浪的特征)。自5科艾略特波浪的简单模式:推动浪、倾斜三角形驱动浪 、锯齿形调整浪、平台形调整浪和三角形调整浪。有13种简单模式的变体:推动浪、终结倾 斜三角形驱动浪、引导倾斜三角形驱动浪、锯齿形调整浪、双锯齿形调整浪、三锯齿形调 整浪、规则平台形调整浪、扩散平台形调整浪、顺势平台形调整浪、收缩三角形调整浪、 下降三角形调整浪、上升三角形调整浪、扩散三角形调整浪。 调整方式有两组:简单调整和联合形调整,使组的总数达到3。有2 目联合形调整(双重调整 和三重调整),使目的总数达到5。如果允许每个联合形调整浪中只有一个三角形调整浪, 以及每个联合形调整浪中只有一个锯齿形调整浪(这是必须的),总共就会有8科联合形调 整浪:锯齿形/平台形、锯齿形/三角形、平台形/平台形、平台形/三角形、锯齿形/平台 形/平台形、锯齿形/平台形/三角形、平台形/平台形/平台形和平台形/平台形/ 三角形,它们使科的总数达到13。简单模式和联合形的总科数是21。 图3一14是这种复杂结构的发展树。在图中,联合形态的排列组合,或波浪中的次要变体 如哪一浪延长了(如果存在),什么方法能满足交替,一个推动浪是否包含倾斜三角形驱动 浪,每个联合形 态中的三角形都属于哪些类型等等,都可以使这种发展继续下去。 这个排列过程可能有一种人为修饰的因素,因为准都能按可接受的分类构造出一些可能 的变体。尽管如此,作为一种反映斐波纳奇序列的原理看起来反映了斐波纳奇序列有关 的原理本身是值得引见的。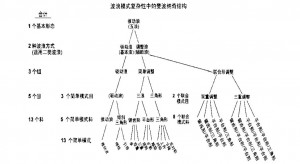
φ与加性增长 正如我们将在后续章节中展示的那样,市场活动受黄金比率的控制。即使是市场统计 数据中的斐波纳奇数字也比概率允许出现的多。然而,关键必须明白,在波浪理论的大概 念中,数字本身确实有理论上的重要性,而只有比率才是这种生长模式的基本关键。尽管 在文献中很少指出,但无论序列从哪两个数字开始,这种类型的加性序列产生了斐波纳 奇比率。斐波纳奇序列是其自身类型的基本加性序列,因为它从数字1开始(见图3— 15),而1是数学增长的起点。然而,我们可以任意选取两个数字,如17和352,然后将它们 相加得到第三个数字,并按这种方法产生更多的数字。随着这个序列的发展,序列中相邻 两项的比率总是很快接近极限φ。当第八项产生的时候,这种关系就变得十分明显(见图3 — 16)。因此,产生斐波纳奇序列的特定数字反映了市场中理想的波浪行进,而斐波纳奇比 率是儿何图形行进的基本法则,在这个行进中前面两个单位加起来产生了下一个单位。 这就是为什么这个比率主宰着如此之多的与生长和衰退,扩散和收缩,以及前进和后退 的自然现象有关的数据。 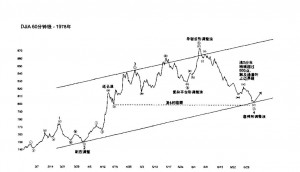
从最广的意义上说,艾略特波浪理论认为塑造生物和星系外形的相同法则,是人类群 体的灵瑰和活动所固有的。因为股票市场是世界上最好的大众心理反射器,所以它的数 据是对人类心理状态和趋势的最佳记录。这种人类生产企业自我估价波动的记录,证明 了前进与倒退的各种特定模式。波浪理论说的是,人类的行进(股票市场是对此的一种大 众确定的估价)不是呈一条直线,也不是随机地发生,更不是循环地发生。倒不如说,这种 行进是呈“三步前进,二步后退”的方式,这是一种自然界青睐的形态。更广义地说,因为 人类的社会活动与斐波纳奇序列数字和行进的螺线形模式相联系,所以它对宇宙中有序 生长的普遍法则显然也不例外。在我们看来,波浪理论与其他自然现象的大量相似之处, 仅仅因为有太多的无知而被忽略了。就可能发生的事而言,我们得出的结论是,有一种无 处不在的原理决定着各种社会事务的形态,而且当爱因斯坦说“上帝不和宇宙玩掷色子的 游戏”时知道自己是在谈什么。股票市场也不例外,因为群体行为无可否认地与某种可以 被验证和定义的法则有关。表达这个原理的最简要途径是一个简单的数字:比率1.618。 诗人马克思·埃哈曼(Max Ehrman)在《迫切需要的东西(Desiderata)》一 诗中写到,“你是宇宙的子民,就像树木和星星;你有权来到这个世上。无论对你是否清楚 ,宇宙无疑以它应有的方式展开。”这是生命中的规则?是的。这是股票市场中的规则?显 而易见。
第二部分 艾略特理论的实际应用
1939年,《金融世界》杂志出版了十二篇艾略特撰写的题为《波浪理论》的论文。在介绍这 些论文时,原出版者按是这样说的: 在过去的七、八年里,金融类杂志的出版者和投资顾问领域内的组织实际上已 经淹没在各种各样的 “方法”中了,这些方法的支持者认为它们可以精确地预 测股票市场的运动。其中有些方法曾风光一时。而另一些则很快被证明毫无价 值。 《金融世界》杂志曾对所有的方法持强烈的怀疑态度。但在研究了R·N· 艾略特先生的 《波浪理论》之后, 《金融世界》杂志逐渐确信有关这一主题的 一系列论文将会引起读者的兴趣,并使读者从中受益。确定波浪理论作为市场 预测工具的价值是读者的事,但我们可以相信它至少是一种对按经济因素得出 的结论的有效检验。 —— 《金融世界》编辑 在本书的第二部分,我们将转变这些编辑提出的步骤和论点,即在检验完全基于艾略 特波浪理论的市场预测的过程中,经济因素充其量可以当作一种辅助工具。
 峰汇在线
峰汇在线





