弹性价格货币模型介绍
弹性价格货币模型是现代汇率理论中最早建立的最基础的汇率模型。英文名称:Flexible-Price Monetary Model,是在1975年瑞典斯德哥尔摩附近召开的关于“浮动汇率与稳定政策”的国际研讨会上被提出来的。其主要代表人物有弗兰克尔(J·Frenkel)、穆莎(M·Mussa)、考霍(P·Kouri)、比尔森(J·Bilson)等人。
弹性价格货币模型基本思想:汇率是两国货币的相对价格,而不是两国商品的相对价格,因此汇率水平应主要由货币市场的供求状况决定。
弹性价格货币模型的假设
重要假设:
1、稳定的货币需求方程,即货币需求同某些经济变量存在着稳定的关系;
2、购买力平价持续有效。
假设前提:
1、商品价格具有完全弹性,这就是说,当货币供给量变动时,会引起价格水平的迅速调整,而利率和实际国民收入与货币供给无关,从而不会造成由于利率水平的降低而进一步影响产出;
2、购买力平价成立。
3、资本在国际间的流动是完全自由的,不受任何形式的限制;
4、本国资产和外国资产可以完全替代,两国利率为内生变量,并对广义货币模型中的两国利率作了技术处理,不再是原来的自然对数,而是利率本身。
假设的不足之处:
1、购买力平价。因为购买力平价在70年代西方实行浮动汇率制以来一般是失效的,使得弹性价格货币模型建立在非常脆弱的基础之上。
2、货币需求函数。许多研究显示,主要的西方国家的货币需求极不稳定,以收入和利率为基础的需求函数不能全面反映实际的货币需求变化。
弹性价格货币模型分析形式
弹性价格货币模型的基本形式:
s = (m − m * ) − η(y − y * ) + λ(i − i * ) (1)
弹性价格货币模型的基本形式,它将汇率的决定主要归于三组变量:两国相对货币供给量、相对实际收入和相对利息率。
内容:
S_t=Z_t+\frac{\lambda}{1+\lambda}E_tS_{t+1}
其中
Z_t=\frac{1}{1+\lambda}(k-k^*)+\frac{1}{1+\lambda}(m_t-m_t^*)\frac{\psi}{1+\lambda}-(y_t-y^*_t)即为弹性价格货币分析法的一般货币模型。该模型由两部分组成,一部分是Zt,这部分主要反映了货币供给量、国民收入等经济变量等对汇率的影响,这是对汇率的长期影响因素,另一部分是Etst+1,这部分主要反映了市场预期等短期因素对汇率的影响。模型能较好地解释外汇市场短期汇率的变化。
就长期因素对汇率的影响来看:
①本国货币供给量的增加,会导致本国价格水平迅速的相应提高,由于购买力平价短期成立,因此,价格水平的提高将会带来本国货币的相应贬值。
②在其它因素不变的情况下,当本国国民收入增加时,将会导致货币需求的增加,在现有价格水平上,由于货币供给没有相应增加,支出减少使本国价格水平下降,由于购买力平价关系,导致本国汇率上升。
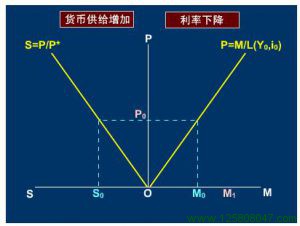
弹性价格分析法也可用上图来表示。假定国外的货币供给、实际收入和利率水平不变,由(1)式知这就决定了国外的价格P^\cdot不变。图1的第一象限反映的是国内货币市场达到均衡时货币供求与价格之间的关系P = M / L(Y,i)。在某一假定的收入和利率水平(Yo,Io)下,货币均衡线P = M / L(Yo,Io)是一条从原点出发的直线。当货币供给从Mo增加到M1时,价格水平同比例上升,由Po上升到P1。图15—3的第二象限反映的是购买力平价线P=SP^\cdot 。由于P^\cdot被假定不变,则S=\frac{P}{P^\cdot}为一条从原点出发的斜率为固定的直线。当国内货币扩张(M_o\to M_1)使得价格上升到(P_o\to P_1)时,汇率就会相应地被由So提高到S1,本币贬值。
 峰汇在线
峰汇在线